Capacitively Coupled Charge Qubits

This project started in the Fall of 2014, focusing on the operation of two or more charge qubits which are capacitively coupled.

General Formulation

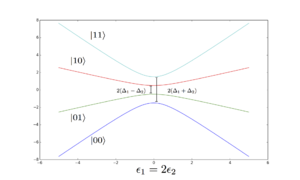
Energy levels of the 2 qubit system as a function of both detunings.

For a single charge qubit, the Hamiltonian is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle H_i = \left( \begin{matrix} \epsilon_i/2 & \Delta_i \\ \Delta_i & -\epsilon_i/2 \end{matrix}\right) }

We will refer to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_i} as the detuning and tunnel coupling of qubit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} , respectively.

We can further write down the full Hamiltonian explicitly:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle H = \left( \begin{matrix} \frac{1}{2}(\epsilon_1+\epsilon_2) + g & \Delta_2 & \Delta_1 & 0 \\ \Delta_2 & \frac{1}{2}(\epsilon_1-\epsilon_2) - g & 0 & \Delta_1 \\ \Delta_1 & 0 & \frac{1}{2}(-\epsilon_1+\epsilon_2) - g & \Delta_2 \\ 0 & \Delta_1 & \Delta_2 & \frac{1}{2}(-\epsilon_1-\epsilon_2) + g \end{matrix}\right) }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g} is the capacitive coupling between the qubits.

Sweet Spots

A major issue with charge qubits is that they are very susceptible to charge noise, which occurs when charge fluctuations outside the system induce undesired shifts in the parameters of the Hamiltonian. The goal of a sweet spot is to find a point in the parameter space where the energy levels are as invariant to the shifts as possible.

First Order Detuning Noise

The most dominant noise source is due to the shifts in the detuning. It is believed that the only point at which the first order dependence on the detunings disappears is at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_1 = \epsilon_2 = 0} . This has been confirmed analytically in the limit of small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g} , and no exceptions have been observed numerically.

• 

  Gap between 01 and 10 states

• 

  Gap between 00 and 11 states

• 

  Gap between 00 and 01 states

• 

  Gap between 00 and 10 states

Second Order Detuning Noise

For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_2 = 0} , we have the following energy levels:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda_1 = -\sqrt{\Delta_1^2+\Delta_2^2+\frac{\epsilon_1^2}{4}+g^2+\sqrt{4\Delta_1^2\Delta_2^2+\epsilon_1^2(\Delta_2^2+g^2)}} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda_2 = -\sqrt{\Delta_1^2+\Delta_2^2+\frac{\epsilon_1^2}{4}+g^2-\sqrt{4\Delta_1^2\Delta_2^2+\epsilon_1^2(\Delta_2^2+g^2)}} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda_3 = \sqrt{\Delta_1^2+\Delta_2^2+\frac{\epsilon_1^2}{4}+g^2-\sqrt{4\Delta_1^2\Delta_2^2+\epsilon_1^2(\Delta_2^2+g^2)}} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda_4 = \sqrt{\Delta_1^2+\Delta_2^2+\frac{\epsilon_1^2}{4}+g^2+\sqrt{4\Delta_1^2\Delta_2^2+\epsilon_1^2(\Delta_2^2+g^2)}} }

which to second order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_1} are:

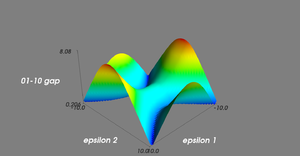
Energy gap between 01 and 10 states as a function of both detunings. Here, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_1 = 2} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_2 = 1} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g = 1} , so the gap is invariant to second-order fluctuations in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_1} .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda_1 \approx \lambda_1^0 + \frac{\Delta_2(\Delta_1+\Delta_2)+g^2}{8\Delta_1\Delta_2\lambda_1^0}\epsilon_1^2 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda_2 \approx \lambda_2^0 + \frac{\Delta_2(\Delta_1-\Delta_2)-g^2}{8\Delta_1\Delta_2\lambda_2^0}\epsilon_1^2 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda_3 \approx \lambda_3^0 + \frac{\Delta_2(\Delta_1-\Delta_2)-g^2}{8\Delta_1\Delta_2\lambda_3^0}\epsilon_1^2 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda_4 \approx \lambda_4^0 + \frac{\Delta_2(\Delta_1+\Delta_2)+g^2}{8\Delta_1\Delta_2\lambda_4^0}\epsilon_1^2 }

The second order terms cannot be tuned such that all gaps are invariant to second order noise. However, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g} can be tuned such that some of the transitions become invariant to some of the second order detuning shifts. To make the transition between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |01\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |10\rangle} flat with respect to second order fluctuations in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_1} , we can set

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g^2 = \Delta_2(\Delta_1-\Delta_2) }

Unfortunately, none of the other transitions can be made to be invariant to second order fluctuations in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_1} . Also, If we wish to make this transition invariant to all second order detuning fluctuations, we must set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_1 = \Delta_2} , making Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g = 0} .

Tunnel Coupling and Capacitive Coupling Noise

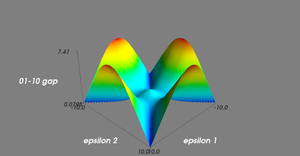
Energy gap between 01 and 10 states as a function of both detunings. Here, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta_1= \Delta_2 = 1} . Although the second order effects of the detunings are non-zero, they are relatively small.

Assuming that we sit at the sweet spot Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_1 = \epsilon_2 = 0} , the energies are relatively simple, so we can easily see the effect of noise on the other parameters.

State	Energy	Effect of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \delta\Delta_1}	Effect of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \delta g}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |00\rangle}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -\sqrt{(\Delta_1+\Delta_2)^2 + g^2}}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -\frac{(\Delta_1+\Delta_2)}{\sqrt{(\Delta_1+\Delta_2)^2 + g^2}}\delta\Delta_1}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -\frac{g}{\sqrt{(\Delta_1+\Delta_2)^2 + g^2}}\delta g}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |01\rangle}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -\sqrt{(\Delta_1-\Delta_2)^2 + g^2}}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -\frac{(\Delta_1-\Delta_2)}{\sqrt{(\Delta_1-\Delta_2)^2 + g^2}}\delta\Delta_1}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -\frac{g}{\sqrt{(\Delta_1-\Delta_2)^2 + g^2}}\delta g}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |10\rangle}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sqrt{(\Delta_1-\Delta_2)^2 + g^2}}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{(\Delta_1-\Delta_2)}{\sqrt{(\Delta_1-\Delta_2)^2 + g^2}}\delta\Delta_1}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{g}{\sqrt{(\Delta_1-\Delta_2)^2 + g^2}}\delta g}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |11\rangle}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sqrt{(\Delta_1+\Delta_2)^2 + g^2}}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{(\Delta_1+\Delta_2)}{\sqrt{(\Delta_1+\Delta_2)^2 + g^2}}\delta\Delta_1}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{g}{\sqrt{(\Delta_1+\Delta_2)^2 + g^2}}\delta g}

Note that if we want any of the transitions to be invariant to first-order fluctuations in tunnel coupling, we would need to set either $\Delta _{1}$ or $\Delta _{2}$ to zero or set $\Delta _{1}=\Delta _{2}$. The first change would make the energy levels degenerate, which must be avoided. If we set the tunnel couplings to be equal, it would be impossible to make any of the transitions invariant to second order effects in the detuning.

There is nothing we can do short of making the energy levels degenerate to make the transitions invariant with respect to first-order fluctuations in capacitive coupling. We could, however, make the coupling itself as stable as possible through manipulating the geometry of the system.

Rotations

SECTION IN PROGRESS

After bringing the system adiabatically to the sweet spot $\epsilon _{1}=\epsilon _{2}=0$, we can apply an AC pulse to some of our parameters to induce a rotation within the system.

AC Pulse	Resulting Matrix (Lab Basis)	Resulting Matrix (Energy Basis)
$\epsilon _{1}$	${\frac {1}{2}}\left({\begin{matrix}B&0&0&0\\0&B&0&0\\0&0&-B&0\\0&0&0&-B\end{matrix}}\right)\cos {(\omega _{AC}t)}$	${\frac {1}{2}}\left({\begin{matrix}0&A_{1}&A_{2}&0\\A_{1}&0&0&A_{3}\\A_{2}&0&0&A_{4}\\0&A_{3}&A_{4}&0\end{matrix}}\right)\cos {(\omega _{AC}t)}$
$\epsilon _{2}$	${\frac {1}{2}}\left({\begin{matrix}B&0&0&0\\0&-B&0&0\\0&0&B&0\\0&0&0&-B\end{matrix}}\right)\cos {(\omega _{AC}t)}$	${\frac {1}{2}}\left({\begin{matrix}0&0&B&0\\0&0&0&B\\B&0&0&0\\0&B&0&0\end{matrix}}\right)\cos {(\omega _{AC}t)}$
$\Delta _{1}$	${\frac {1}{2}}\left({\begin{matrix}0&0&B&0\\0&0&0&B\\B&0&0&0\\0&B&0&0\end{matrix}}\right)\cos {(\omega _{AC}t)}$	${\frac {1}{2}}\left({\begin{matrix}-B{\frac {\Delta _{1}+\Delta _{2}}{\lambda _{1}}}&0&0&-B{\frac {g}{\lambda _{1}}}\\0&-B{\frac {\Delta _{1}-\Delta _{2}}{\lambda _{2}}}&-B{\frac {g}{\lambda _{2}}}&0\\0&-B{\frac {g}{\lambda _{2}}}&B{\frac {\Delta _{1}-\Delta _{2}}{\lambda _{2}}}&0\\-B{\frac {g}{\lambda _{1}}}&0&0&B{\frac {\Delta _{1}+\Delta _{2}}{\lambda _{1}}}\end{matrix}}\right)\cos {(\omega _{AC}t)}$
$\Delta _{2}$	${\frac {1}{2}}\left({\begin{matrix}0&B&0&0\\B&0&0&0\\0&0&0&B\\0&0&B&0\end{matrix}}\right)\cos {(\omega _{AC}t)}$	${\frac {1}{2}}\left({\begin{matrix}0&0&B&0\\0&0&0&B\\B&0&0&0\\0&B&0&0\end{matrix}}\right)\cos {(\omega _{AC}t)}$