This project started in the Fall of 2014, focusing on the operation of two or more charge qubits which are capacitively coupled. Current PDF Summary can be found File:Capacitively Coupled Qubits.pdf
General Formulation
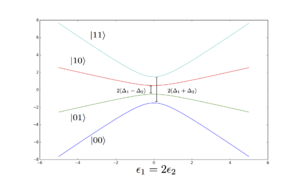
Energy levels of the 2 qubit system as a function of both detunings.
For a single charge qubit, the Hamiltonian is

We will refer to  and
and  as the detuning and tunnel coupling of qubit
as the detuning and tunnel coupling of qubit  , respectively.
, respectively.
We can further write down the full Hamiltonian explicitly:

where  is the capacitive coupling between the qubits.
is the capacitive coupling between the qubits.
Sweet Spots
A major issue with charge qubits is that they are very susceptible to charge noise, which occurs when charge fluctuations outside the system induce undesired shifts in the parameters of the Hamiltonian. The goal of a sweet spot is to find a point in the parameter space where the energy levels are as invariant to the shifts as possible.
First Order Detuning Noise
The most dominant noise source is due to the shifts in the detuning. It is believed that the only point at which the first order dependence on the detunings disappears is at  . This has been confirmed analytically in the limit of small
. This has been confirmed analytically in the limit of small  , and no exceptions have been observed numerically.
, and no exceptions have been observed numerically.
Gap between 01 and 10 states
Gap between 00 and 11 states
Gap between 00 and 01 states
Gap between 00 and 10 states
Second Order Detuning Noise
For  , we have the following energy levels:
, we have the following energy levels:




which to second order in  are:
are:
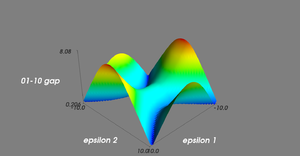
Energy gap between 01 and 10 states as a function of both detunings. Here,

,

, and

, so the gap is invariant to second-order fluctuations in

.




The second order terms cannot be tuned such that all gaps are invariant to second order noise. However,  can be tuned such that some of the transitions become invariant to some of the second order detuning shifts. To make the transition between
can be tuned such that some of the transitions become invariant to some of the second order detuning shifts. To make the transition between  and
and  flat with respect to second order fluctuations in
flat with respect to second order fluctuations in  , we can set
, we can set

Unfortunately, none of the other transitions can be made to be invariant to second order fluctuations in  . Also, If we wish to make this transition invariant to all second order detuning fluctuations, we must set
. Also, If we wish to make this transition invariant to all second order detuning fluctuations, we must set  , making
, making  .
.
Tunnel Coupling and Capacitive Coupling Noise
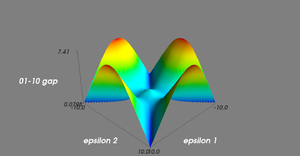
Energy gap between 01 and 10 states as a function of both detunings. Here,

. Although the second order effects of the detunings are non-zero, they are relatively small.
Assuming that we sit at the sweet spot  , the energies are relatively simple, so we can easily see the effect of noise on the other parameters.
, the energies are relatively simple, so we can easily see the effect of noise on the other parameters.
| State
|
Energy
|
Effect of 
|
Effect of 
|
 |
 |
 |

|
 |
 |
 |

|
 |
 |
 |

|
 |
 |
 |

|
Note that if we want any of the transitions to be invariant to first-order fluctuations in tunnel coupling, we would need to set either  or
or  to zero or set
to zero or set  . The first change would make the energy levels degenerate, which must be avoided. If we set the tunnel couplings to be equal, it would be impossible to make any of the transitions invariant to second order effects in the detuning.
. The first change would make the energy levels degenerate, which must be avoided. If we set the tunnel couplings to be equal, it would be impossible to make any of the transitions invariant to second order effects in the detuning.
There is nothing we can do short of making the energy levels degenerate to make the transitions invariant with respect to first-order fluctuations in capacitive coupling. We could, however, make the coupling itself as stable as possible through manipulating the geometry of the system.
Rotations
Shifting to the Rotating Frame
After bringing the system adiabatically to the sweet spot  , we can apply an AC pulse to some of our parameters to induce a rotation within the system.
, we can apply an AC pulse to some of our parameters to induce a rotation within the system.
| AC Pulse
|
Resulting Matrix (Lab Basis)
|
Resulting Matrix (Energy Basis)
|
 |
 |

|
 |
 |

|
 |
 |

|
 |
 |

|
where  ,
,  , and
, and  ,
,  ,
,  , and
, and  are all complicated functions of the parameters which are discussed below.
are all complicated functions of the parameters which are discussed below.
Based off of the rotation matrices in the energy basis, it's clear that the situation in which  fundamentally differs from the case in which
fundamentally differs from the case in which  . Moreover, it can be seen that the case in which
. Moreover, it can be seen that the case in which  yields diverging results (as some of the matrix elements feature a step function at this point). So in practice, it would be good to avoid this point. Writing the rotations explicitly for the two regimes:
yields diverging results (as some of the matrix elements feature a step function at this point). So in practice, it would be good to avoid this point. Writing the rotations explicitly for the two regimes:
| AC Pulse
|
Energy Basis ( ) )
|
Energy Basis ( ) )
|
 |
 |

|
 |
 |

|
 |
 |

|
 |
 |

|
We can further analyze these matrices by considering the effective rotations in the rotating frame for different applied frequencies, using the rotating wave approximation:
| AC Pulse
|
Rotating Frame ( ) )
|
Rotating Frame ( ) )
|
 |
 |
 |

|
 |
 |

|
 |
 |
 |

|
 |
 |

|
 |
 |
 |

|
 |
 |

|
 |
 |
 |

|
 |
 |

|
Constructing Logical Gates
We will assume in this section that we are in the regime  . The same gates can be determined in the other regime as well.
. The same gates can be determined in the other regime as well.
 gate (
gate ( on qubit 1)
on qubit 1)
- Wait for a time
 (always on)
(always on)
 gate (
gate ( on qubit 2)
on qubit 2)
- Wait for a time
 (always on)
(always on)
 gate (
gate ( on qubit 1)
on qubit 1)
- Pulse
 at a frequency of
at a frequency of  for a time
for a time 
 gate (
gate ( on qubit 2)
on qubit 2)
- Pulse
 at a frequency of
at a frequency of  for a time
for a time 
 gate (
gate ( with qubit 1 as control)
with qubit 1 as control)
- Pulse
 at a frequency of
at a frequency of  for a time
for a time 
- Pulse
 at a frequency of
at a frequency of  for a time
for a time 
 gate (
gate ( with qubit 2 as control)
with qubit 2 as control)
- Pulse
 at a frequency of
at a frequency of  for a time
for a time 
- Pulse
 at a frequency of
at a frequency of  for a time
for a time 

- Pulse either
 or
or  at a frequency of
at a frequency of  for a time
for a time 
Notes on Logical Operating Points
Here we discuss the values of  ,
,  ,
,  , and
, and  . Analytical expressions can and have been found for these quantities, but they yield little intuition about their nature.
. Analytical expressions can and have been found for these quantities, but they yield little intuition about their nature.
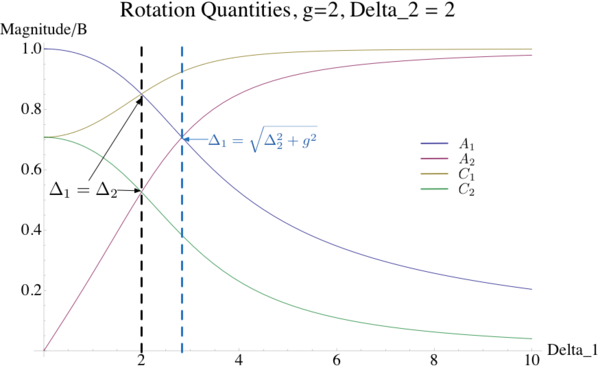
Above is a graph of the 4 values as a function of  . If we wish to consider the regime in which
. If we wish to consider the regime in which  as above, we should consider the part of the graph to the right of the black dotted line.
as above, we should consider the part of the graph to the right of the black dotted line.
A few qualitative statements can be made about the logical gates based off of this graph. First, it is clear that the  gate will always be faster than the
gate will always be faster than the  gate. A feature of concern is the behavior of
gate. A feature of concern is the behavior of  , namely that it tends towards zero, as this increases the time for the
, namely that it tends towards zero, as this increases the time for the  gate.
gate.
Numerical Simulations
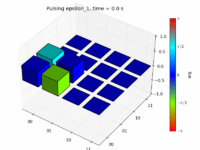
Animation of the density matrix during the application of the X1 gate
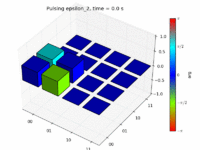
Animation of the density matrix during the application of the X2 gate
Using the QuTiP package, we can simulate the Master Equation for the system in question. First, we can verify the gates that we proposed under ideal conditions. Below are pictures of the density matrix as it undergoes pulses that we have predicted to correspond to X1 and X2 gates. Note that the behavior of the density matrix matches what we would expect.
Animations of these transformations can be found on the right.
Issues with CNOT gate:
Superpostition between 00 and 01 state







































































































