|
Size: 4318
Comment:
|
← Revision 20 as of 2018-07-18 16:57:58 ⇥
Size: 4145
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| ||<:30%>[:PiraScheme#Mechanics: Table of Mechanics Demonstration]||<:30%>[:MEEquipmentList: List of Mechanics Equipment & Supplies]||<:30%>[:Demonstrations:Lecture Demonstrations]|| | ||<30% style="text-align:center">[[PiraScheme#Mechanics|Table of Mechanics Demonstration]] ||<30% style="text-align:center">[[MEEquipmentList|List of Mechanics Equipment & Supplies]] ||<30% style="text-align:center">[[Demonstrations|Lecture Demonstrations]] || |
| Line 5: | Line 6: |
| '''Topic and Concept:''' | |
| Line 6: | Line 8: |
| '''Topic and Concept:''' [:AppNewtonsLaws#DynamicTorque: 1K10. Applications of Newton's Laws, Dynamic Torque] |
. [[AppNewtonsLaws#DynamicTorque|1K10. Applications of Newton's Laws, Dynamic Torque]] '''pira200 Listed''' |
| Line 10: | Line 13: |
| * '''Cabinet:''' [:MechanicsCabinet:Mechanic (ME)] * '''Bay:''' [:MechanicsCabinetBayA9:(A9)] * '''Shelf:''' #2 |
|
| Line 14: | Line 14: |
| attachment:WalkingSpool01-400.jpg | * '''Cabinet:''' [[MechanicsCabinet|Mechanic (ME)]] * '''Bay:''' [[MechanicsCabinetBayA9|(A9)]] * '''Shelf:''' #2 {{attachment:WalkingSpool01-400.jpg}} |
| Line 18: | Line 22: |
| Pull on a cord wrapped around the axle of a large spool. The spool can be made to go forward or backward depending on the relative angle of applied torque. ||<:style="width: 60%" :40%>'''Equipment'''||<:30%>'''Location'''||<:25%>'''ID Number'''|| |
Pull on a cord that is wrapped around the axle of a large spool. The spool can be made to either roll forward, roll backward, or slide forward depending on the relative angle of applied force to the spool's axle. ||<40% style="" ;text-align:center">'''Equipment''' ||<30% style="text-align:center">'''Location''' ||<25% style="text-align:center">'''ID Number''' || |
| Line 22: | Line 25: |
| ||Spool w/String||[:MechanicsCabinetBayA9: ME, Bay A9, Shelf #2 & 4]|| || | ||Walking Spool, a ||[[MechanicsCabinetBayA9|ME, Bay A9, Shelf #2]] ||1K10.30a || ||Walking Spool, b ||[[MechanicsCabinetBayA9|ME, Bay A9, Shelf #4]] ||1K10.30b || |
| Line 25: | Line 29: |
| '''''Important Setup Notes:''''' * This demonstration may require practice. |
|
| Line 29: | Line 31: |
| '''Setup and Procedure:''' | '''''Important Setup Notes:''''' |
| Line 31: | Line 33: |
| 1. Unravel enough of the string from the spool so that the audience can see you pull on the string. | * This demonstration may require practice to find the critical angle. '''Setup and Procedure:''' 1. Unravel enough of the string from the spool so that the audience can see you pull on the string. |
| Line 33: | Line 39: |
| 1. Apply a torque to the spool by pulling on the string. Try a mainly horizontal pull to make the spool move toward you. There is a critical angle as the string is pulled in a more upward direction whereupon the spool will begin to "walk" away from you. | 1. When placing the pool on a table, make sure that the string's tangent point to the axle is below the central axis of rotation. 1. Apply a torque to the spool by pulling on the string. Try a mainly horizontal pull to make the spool move toward you. There is a critical angle as the string is pulled in a more upward direction whereupon the spool will begin to "walk" away from you. |
| Line 36: | Line 43: |
| Line 38: | Line 46: |
| '''Discussion:''' | |
| Line 39: | Line 48: |
| '''Discussion:''' | In order to make the spool "walk", a force must be applied to it to accelerate it into motion. In our case, this is a torque caused by the tension in the string. The magnitude of this torque is equal to the radius of the axle of the spool multiplied by the product of the tension and the sine of angle the sting makes with the radial line drawn to the point of contact. This is illustrated in the diagram from Wikipedia below. The walking direction that the spool assumes is decided by the balance of torques acting on the spool. |
| Line 41: | Line 50: |
| In order to make the spool "walk", a force must be applied to it to accelerate it into motion. In our case, this is a torque caused by the tension in the string. The magnitude of this torque is equal to the radius of the axle of the spool multiplied by the product of the tension and the sine of angle the sting makes with the radial line drawn to the point of contact. This is illustrated in the diagram from Wikipedia below. The walking direction that the spool assumes is decided by the balance of torques acting on the spool. attachment:walking_the_spool_fbd-250.jpg |
{{attachment:walking_the_spool_fbd-250.jpg}} |
| Line 53: | Line 60: |
| Here, we have assumed that the torques are applied at right angles relative to the radial vector. From (1), we get that | Here, we have assumed that the torques are applied at right angles relative to the radial vector. From (1), we get that |
| Line 60: | Line 67: |
| || {{attachment:WalkingSpool02-250.jpg}} || {{attachment:WalkingSpool03-250.jpg}} || {{attachment:WalkingSpool04-250.jpg}} || || {{attachment:WalkingSpool05-250.jpg}} || {{attachment:WalkingSpool06-250.jpg}} || {{attachment:torque-250.png}} || |
|
| Line 61: | Line 70: |
| ||attachment:WalkingSpool02-250.jpg||attachment:WalkingSpool03-250.jpg||attachment:WalkingSpool04-250.jpg|| ||attachment:WalkingSpool05-250.jpg||attachment:WalkingSpool06-250.jpg||attachment:torque-250.png|| |
|
| Line 65: | Line 74: |
| * [https://www.youtube.com/user/LectureDemostrations/videos?view=1 Lecture Demonstration's Youtube Channel] | * [[https://www.youtube.com/user/LectureDemostrations/videos?view=1|Lecture Demonstration's Youtube Channel]] |
| Line 69: | Line 79: |
| * [https://en.wikipedia.org/wiki/Torque Wikipedia - Torque] * [http://scienceblogs.com/dotphysics/2010/01/27/yo-yo-rolling-sliding-pulling/ Scienceblogs.com - Yo Yo Problem] |
* [[https://en.wikipedia.org/wiki/Torque|Wikipedia - Torque]] * [[http://scienceblogs.com/dotphysics/2010/01/27/yo-yo-rolling-sliding-pulling/|Scienceblogs.com - Yo Yo Problem]] |
| Line 72: | Line 82: |
---- /!\ '''Edit conflict - other version:''' ---- ---- /!\ '''Edit conflict - other version:''' ---- * [http://scienceblogs.com/dotphysics/2010/01/27/yo-yo-rolling-sliding-pulling/ Scienceblogs.com - Yo Yo Problem] ---- /!\ '''Edit conflict - your version:''' ---- ---- /!\ '''End of edit conflict''' ---- [:Instructional:Home] ---- /!\ '''Edit conflict - your version:''' ---- ---- /!\ '''Edit conflict - other version:''' ---- * [http://scienceblogs.com/dotphysics/2010/01/27/yo-yo-rolling-sliding-pulling/ Scienceblogs.com - Yo Yo Problem] ---- /!\ '''Edit conflict - your version:''' ---- ---- /!\ '''End of edit conflict''' ---- [:Instructional:Home] ---- /!\ '''End of edit conflict''' ---- |
[[Instructional|Home]] |
Walking the Spool, 1K10.30
Topic and Concept:
pira200 Listed
Location:
Cabinet: Mechanic (ME)
Bay: (A9)
Shelf: #2

Abstract:
Pull on a cord that is wrapped around the axle of a large spool. The spool can be made to either roll forward, roll backward, or slide forward depending on the relative angle of applied force to the spool's axle.
Equipment |
Location |
ID Number |
|
|
|
Walking Spool, a |
1K10.30a |
|
Walking Spool, b |
1K10.30b |
Important Setup Notes:
- This demonstration may require practice to find the critical angle.
Setup and Procedure:
- Unravel enough of the string from the spool so that the audience can see you pull on the string.
- Place the pool on a table so that the axle is horizontal as seen in the main photo above.
- When placing the pool on a table, make sure that the string's tangent point to the axle is below the central axis of rotation.
- Apply a torque to the spool by pulling on the string. Try a mainly horizontal pull to make the spool move toward you. There is a critical angle as the string is pulled in a more upward direction whereupon the spool will begin to "walk" away from you.
Cautions, Warnings, or Safety Concerns:
- N/A
Discussion:
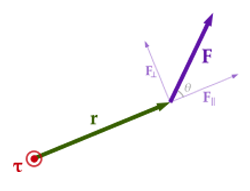
In order to make the spool "walk", a force must be applied to it to accelerate it into motion. In our case, this is a torque caused by the tension in the string. The magnitude of this torque is equal to the radius of the axle of the spool multiplied by the product of the tension and the sine of angle the sting makes with the radial line drawn to the point of contact. This is illustrated in the diagram from Wikipedia below. The walking direction that the spool assumes is decided by the balance of torques acting on the spool.
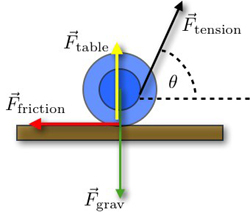
As a special case, consider the situation where we are at the critical angle where the spool does not spin and that we are dragging it across the table at constant speed. Then we can assume a constant friction force acting on the spool. Our equations of motion then are
(1) τnet= 0 = ri·T - r0·f = ri·T - r0·μk·m·g, the i and o denote the inner and outer radii, T is the tension, f is the friction
(2) Fx = 0 = T·cos(θ)-μk·m·g
(3) Fy = 0 = T·sin(θ)-m·g
Here, we have assumed that the torques are applied at right angles relative to the radial vector. From (1), we get that
T = (r0·μk·m·g)/ri
Plugging this into (2) and solving for θ, we see that θC = cos-1(ri/r0)
For the red & blue spool, ri = 3.8 cm and r0 = 9.9 cm which gives θC = 67°.
|
|
|
|
|
|
Videos:
References: