Conical Pendulum, 1D50.25
Topic and Concept:
Motion in Two Dimensions, 1D50. Central Forces
Location:
Cabinet: Mechanic (ME)
Bay: (A7)
Shelf: #1


Abstract:
A wire is suspended from a ceiling mount and a bowling ball attached at the bottom. It is then put into an elliptical orbit thus acting as a conical pendulum.
Equipment |
Location |
ID Number |
|
|
|
Bowling Ball |
ME, Bay A7, Shelf #1 |
|
Wire |
Appropriate Wires in Each Lecture Hall, Backups in ME, Bay B , Shelf # |
|
Wood Hanging Rod |
Located Near Rod & Tack Cabinet by Main Lecture Halls |
|
Ball On String |
ME, Bay B1, Shelf #2 |
|
Rod/Clamp Assembly |
Rod & Tack Cabinet Located Near Main Lecture Halls |
|
Important Setup Notes:
This demo can be done using the suspended bowling ball or the Simple_Pendulum setup.
- There are two such wires for the bowling ball. The shorter of the two works best for this demonstration.
Setup and Procedure:
If using the simple pendulum setup, see Simple_Pendulum.
- Else, if using the bowling ball, first suspend the wire from the ceiling using the hanging rod.
- Connect the bowling ball to the wire using the attached black clip.
- Pull the bowling ball off center while keeping the wire taught (giving the bowling ball gravitational potential energy).
- Swing the ball in a circular arc to get it in orbit (this is where θ gets set).
Cautions, Warnings, or Safety Concerns:
- If using the bowling ball setup, don't let anyone get in the way of the rotating bowling ball - it has a lot of inertia and will not feel good if it hits someone.
Discussion:
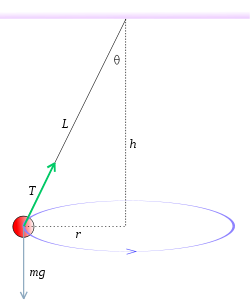
When the bob (tennis, brass, wood, or bowling) is given a push horizontal push, it is given energy which is maintained (ignoring non-conservative forces). It also is given a velocity which is tangent to its elliptical trajectory. As is always the case with elliptical motion, there must be a central force to provide the change in momentum on the body in motion. This central force, specifically centripetal force, is the horizontal component of the tension being provided by wire, quantified by Tx = Ttot * sin(θ) = m * v2 * R where θ is the angle of the wire when in motion relative to its position at rest, m is the mass of the bob, v is its tangential speed, and R is the radius of the circle (assuming a small enough eccentricity this is a good approximation for the ellipse). The vertical component, quantified by Ty = m * g = Ttot * cos(θ), is responsible for maintaining the height of the bob. From this it is easy to see what determines the speed and angle of trajectory of the bob. When the lecturer puts the bob into orbit, he or she is inputting a certain amount of energy. The given height determines the potential energy and the horizontal push determines the speed. Their sum must remain constant as per the law of conservation of energy. The total energy is E = U + K = (1/2) * m * v2 + m * g * L * cos(θ), where L is the length of the wire and g the acceleration due to gravity.
|
|
|
|
|
|
|
|
|
Videos:
References: