|
Size: 9999
Comment:
|
Size: 10104
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
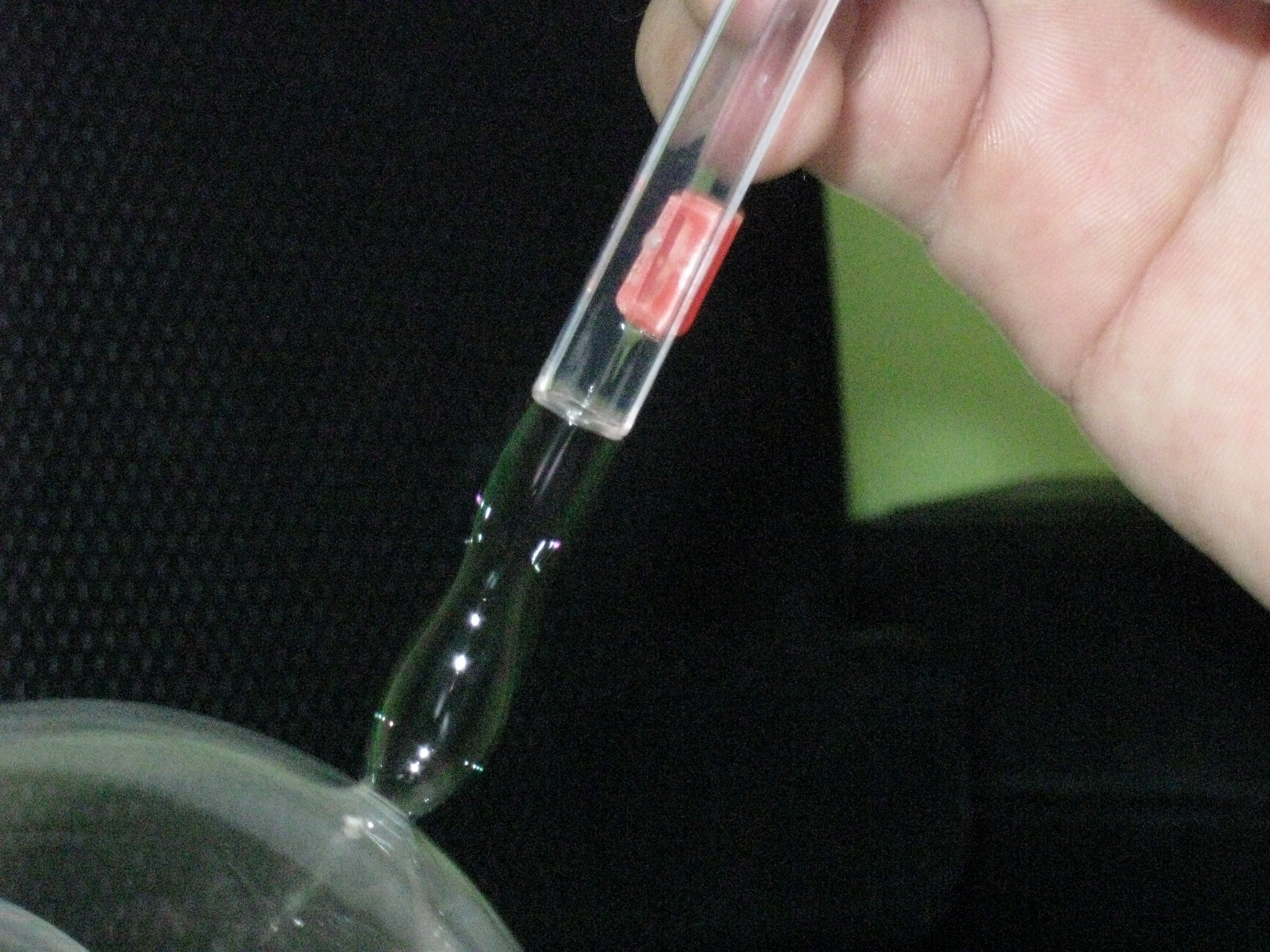
| {{attachment:multinode3.jpg|maybe 3 nodes|width="400"}} {{attachment:double_node.jpg|double node|width="400"}} | {{attachment:multinode3.jpg|maybe 3 nodes|width="400"}} {{attachment:double_node.jpg|double node|width="400"}} {{attachment:cap1.jpg|long tube|width="400"}} {{attachment:dripping.jpg|bubbles 'dripping'|width="400"}} |




I discovered an unusual bubble structure which is unexpectedly very stable. To make it, you blow a hemispherical bubble in a pan of soap water using a straw. Then, while still blowing through the straw, withdraw the straw from the bubble. Under the right conditions, a corrugated tube of soap film will form between the straw and the bubble. The tube collapses when you stop blowing. It can be proved that long cylindrical bubbles are unstable without airflow. As far as I know, nobody has studied bubble stability with airflow. It might be possible to publish a short article about this topic.
Here's what we have for equipment:
*A baking sheet for holding the bubble solution
*Dish detergent, glycerine & distilled water
*Some Tygon tubing attatched to the building air supply
*A single steel tube (ID 4.1mm)
*Digital camera (personal)
*Free image processing software (ImageJ)
Things we might need:
*Straight plastic or metal pipes with a wide range of diameters (1/16" up to 1" or more)
*A variable-area flow meter (~$50 new online)
*A high-speed camera to capture oscillations and break-up
*A way of visualizing the airflow (source of fog, maybe some dry ice or LN2)
*A way to measure the surface tension of the solution
Observations so far:
Blowing the bubbles by hand: In order to make the longest tubes, it's necessary to have a large flow rate, enough to cause audible & visible turbulence inside the tube. It is clear that these tubes are robustly stable, since they can oscillate enough during the turbulent phase to produce sound, without breaking! I think I saw transient states with up to 4 nodes or more. When I reduced the airflow after forming the tube, the number of nodes was reduced, and the turbulence went away. This is how I captured the picture with the distinct 2-node structure.
Blowing the bubbles with the comressed air supply: We used much larger tubes, 3/8" to 1/2" ID, compared to the straws I was using initially. It seemed to be harder to get more than 3 nodes (two anti-nodes), until we increased the concentration of detergent, added glycerine, and used distilled water. We also found that using a metal tube for the nozzle is much better than just blowing the bubbles with the end of a hose (which is curved, and the end is cut at an angle). Finally, tuning the airflow is critical. If the flow is too fast, the airflow is turbulent and this bursts the bubble. At low flow rate, trying to draw out the tube in order to produce more antinodes resulted in oscillations, and the bubble would eventually snap before we could reach the next antinode. With the proper flow rate, it appears to be possible to create tubes of arbitrary length.
Examining the videos shows that the first antinode decreases in diameter when the nozzle is being pulled out to create the longest bubbles. With low flow rate, moving the nozzle slowly closer & farther away causes the first antinode to vanish and re-form with the same shape. It may be important to pull the nozzle away quickly to induce a transition of some kind. Reducing the airflow causes antinodes to have larger diameter (can be much larger than the nozzle), while increased airflow causes the corrugations to flatten, resulting in a tube the same diameter as the nozzle. Reducing the flow also tends to reduce the number of antinodes, indicating that the wavelength of the structure is changing.
A common feature is the tight neck where the tube enters the base bubble. It would be interesting to see if the diameter of this neck changed with airflow rate. It appears to always be as small or smaller than the straw. At high airflow, it is not much, if any, smaller than the rest of the bubble tube.
It is possible to blow at a tangential angle without popping the bubble; in fact, the bubble tube can execute a 90-degree turn! With a bit of luck, you can also produce a stream that breaks up into bubble 'drops,' just like water streams do.
Pictures & Videos
http://www.youtube.com/watch?v=aE_zHbpF3Bo



Experimental Techniques:
Surface tension measurement: We'd like to measure the surface tension in order to compare the surface pressure to the stagnation pressure of the flow.
Bubble pressure method seems simple and accurate: http://dx.doi.org/10.1119/1.3623414
Internal flow velocity measurements: we need a way to measure the flow profiles inside the bubble tube. PIV and LDV are probably the two best choices I've seen. These methods require a bit of work, and also a laser. PIV is nice because it gives a 2-D profile and it goes along well with the goal of measuring the tube dimensions.
Particle image velocimetry: http://tejas.serc.iisc.ernet.in/currsci/jul102000/review%20article.pdf
Laser Doppler velocitimetry: http://link.aip.org/link/doi/10.1119/1.18051?ver=pdfcov
Theory:
Equilibrium: the bubbles appear to be surfaces of roughly-constant 'mean curvature.' This means that the pressure inside the bubbles is also approximately constant along the length, according to the Young-Laplace law and force balance. (This is somewhat puzzling, since Bernoulli's law dictates that the pressure must be lower in the throats, if the flow velocity is higher there.) The pressure in the tube must be higher than in the terminating hemispherical bubble, since the larger bubble has lower curvature. This means that there is some pressure drop across the narrow neck where the tube joins the large bubble. It should be possible to create a long bubble tube with no corrugations if the downstream pressure could be increased, so that the narrow neck was unnecessary. There is also evidently very little pressure drop along the cylindrical part of the tube, so an arbitrarily long tube might be possible. It might also be possible to create a very long corrugated tube by lowering the flow rate of a pre-existing cylindrical tube; however, it may be that pressure loss is incurred at every neck, limiting the length of the tube. It is not clear why the flow rate controls the aspect ratio of the corrugations.
Stability: the constant-mean-curvature surfaces (unduloids) are not stable; they tend to 'neck off' into a string of spheres. That is to say, if the narrow part is pushed in a bit, it is no longer in equilibrium, and it continues to move inward until it collapses. If air is flowing through the neck, it must have a higher velocity as the throat decreases in radius, in order to keep the volumetric flow rate constant. But according to Bernoulli's principle, the pressure is lower where the velocity is higher. This implies that the pressure decreases in the neck, which would accelerate the inward motion of the walls! Clearly this is not the whole story.
Relevant Articles:
Unduloid: a surface with constant mean curvature; they are solutions to the force balance for the case of constant pressure. They look alot like the bubble tubes we're blowing.
Wikipedia has a nice diagram: http://en.wikipedia.org/wiki/Unduloid
Mathematical formula for the unduloid is here: http://www.emis.de/journals/AM/07-5/mladenov.pdf
Description of stability of various forms including unduloids: http://www.math.ucla.edu/~bertozzi/papers/surfdiff98.pdf
Bubble Stability Without Flow: This is what happens without flow. These papers illustrate different techniques for solving the problem.
Analysis of Instability of a Cylindrical Soap Film of Finite Dimensions.http://dx.doi.org/10.1021/la970595k
Stability of interfaces of revolution with constant surface tension—the case of the catenoid. http://dx.doi.org/10.1016/0300-9467(70)85003-1
Stability and oscillations of a soap film: An analytic treatment. http://dx.doi.org/10.1119/1.12506
Good treatment of variational method for bubbles: http://farside.ph.utexas.edu/teaching/336l/fluidhtml/node51.html
Plateau-Rayleigh Instability: This is why a falling stream of water breaks into droplets. There is some similarity, but in our case the surface is not attached to the flow, and there is drag instead of acceleration due to gravity.
Wikipedia has a nice introduction: http://en.wikipedia.org/wiki/Plateau%E2%80%93Rayleigh_instability
On the breakup of viscous liquid thread. http://dx.doi.org/10.1063/1.868540
Nonlinear dynamics and breakup of free-surface flows. http://dx.doi.org/10.1103/RevModPhys.69.865
Lecture notes on surface tension, ch 5. web.mit.edu/1.63/www/Lec-notes/Surfacetension/Lecture5.pdf
Add your name here if you'd like to become involved with the project:
* Lucas Morton
* Bai Yang Wang
* Duncan Carlsmith
Hey Lucas, here is a video of using a speaker to wiggle water. Maybe it will inspire. -duncan
http://www.creativeplanetnetwork.com/dv/news/watch-amazing-video-sound-waves-appearing-water/62003
More inspiration
Engineers explain physics of fluids over 100 years after original discovery,
Dripping honey explained
http://physics.aps.org/articles/v6/38, http://prl.aps.org/abstract/PRL/v110/i14/e144501